1. はじめに
これから製作したいというわけではないのですが、WEBでオーディオ関連のサイトをチェックしていて橋本トランスとノグチトランスのLCRフォノイコライザーコイルが目に入り、その推奨回路図(橋本電気H-EQL)を見ているうちに、その定数でどのような再生カーブが得られるのか解析したくなりました。
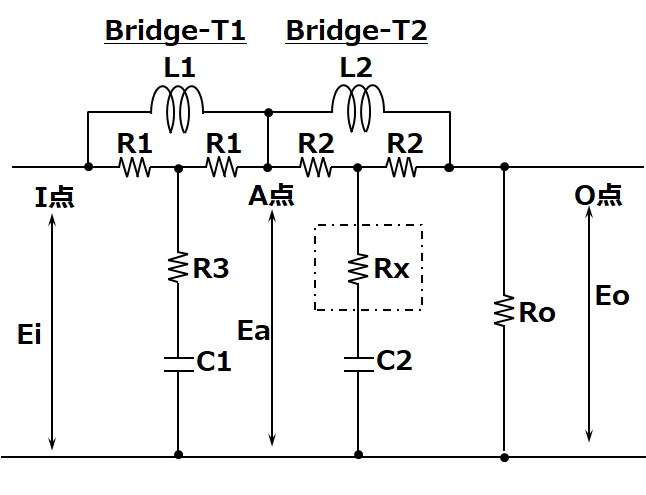
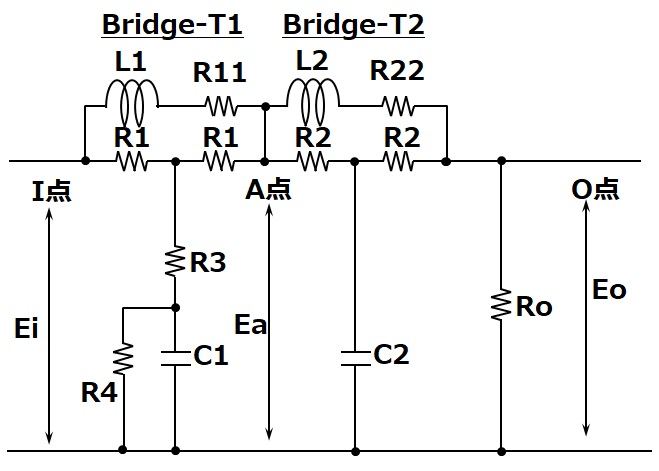
ここに記載した回路はLCRイコライザーを構成する回路の原回路です。LCRイコライザー用コイルには入出力インピーダンス600Ωの条件下でRIAA再生特性を得るために低域用(ターンオーバー)と高域用(ロールオフ)に最適なL(インダクタンス)値が必要となります。
この原回路は1段目、2段目それぞれについて入出力インピーダンス600Ωの定インピーダンス回路です。それぞれの回路を見てみるとブリッジT型の回路構成となっています。これは基本的にブリッジT型アッテネータと同じで、2組の可変抵抗だった部分がLとCに置き換えられています。Totalインピーダンスが一定となる条件下で、アッテネータが抵抗値組み合わせで減衰量を可変させていたことに対して、抵抗値の組み合わせを選定したL,Cに対する周波数応答特性の変化に置き換えていることと同じと考えるのがいいのではないでしょうか。
図内のBridge-T1,Bridge-T2ともに定インピーダンスのブリッジT回路です。すなわち入力I点、中間のA点、出力のO点から負荷(出力)側を見た際のインピーダンスが一定で出力抵抗であるRoと一致します。そのためBridge-T1,2のLCR定数は独立して計算可能で、順序の入れ替えもOKです。
入出力間にL、共通端子側にCが入っているため、このBridge-T1,2の回路は周波数が上昇すると出力が低下することは感覚的にもつかめることと思います。
2. Bridge-T1回路の解析
計算を簡易化する為、上記のBridge-T回路を下記のY型回路に変換します。
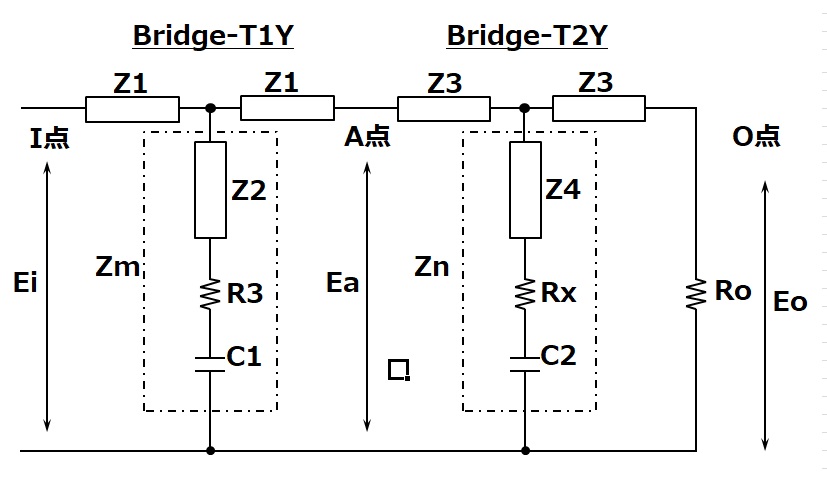
Δ-Y変換に関しては単純に変換公式にしたがって算出します。
Z1=j*ω*L1*R1/(j*ω*L1+2*R1) 式 (2.1)
Z2=R1^2/(j*ω*L1+2*R1) 式 (2.2)
Zm=Z2+R3+1/(j*ω*C1) 式 (2.3)
A点から負荷側を見たインピーダンスは最終的な負荷と同じになるので次段(Bridge-T2)と関係なくRoとなります。
入力側I点から見たインピーダンスもRoとなるので
Ztotal=Ro=Z1+Zm//(Z1+Ro)=Z1+Zm*(Z1+Ro)/(Z1+Zm+Ro) 式 (2.4)
(Ro-Z1)*(Z1+Zm+Ro)=Zm*(Z1+Ro)
Ro^2-Z1^2+Zm*(Ro-Z1)=Zm*(Z1+Ro)
Ro^2=Z1^2+Zm*(Z1+Ro-Ro+Z1)
Ro^2=Z1*(Z1+2*Zm) 式 (2.6)
Zm=(Ro^2-Z1^2)/(2*Z1) 式 (2.7)
2*Z1*Zm=Ro^2-Z1^2
Ro^2=2*Z1*Zm+Z1^2
ここでZ1,Z2の分母をを有理化しておき、さらにZmを計算します。
Z1=(j*ω*L1*R1)/(2*R1+j*ω*L1)
=(j*ω*L1*R1)*(2*R1-j*ω*L1)/( (2*R1)^2-(j*ω*L1)^2 )
=(ω^2*L1^2*R1+j*2*ω*L1*R1^2)/( (ω*L1)^2+(2*R1)^2 )
=(ω^2*L1^2*R1+j*2*ω*L1*R1^2)/(ω^2*L1^2+4*R1^2)
=ω*L1*R1*(ω*L1+2*j*R1)/(ω^2*L1^2+4*R1^2)
Z1=R1*ω*L1*(ω*L1+2*j*R1)/(ω^2*L1^2+4*R1^2) 式 (2.8)
Z2=R1^2/(2*R1+j*ω*L1)
=R1^2*(2*R1-j*ω*L1)/((2*R1+j*ω*L1)*(2*R1-j*ω*L1))
=R1^2*(2*R1-j*ω*L1)/(ω^2*L1^2+4*R1^2) 式 (2.9)
Zm=Z2+R3+1/(j*ω*C1)
=R1^2*(2*R1-j*ω*L1)/(ω^2*L1^2+4*R1^2)+R3+1/(j*ω*C1)
=(R1^2*(2*R1-j*ω*L1)+R3*(ω^2*L1^2+4*R1^2)+(ω^2*L1^2+4*R1^2)/(j*ω*C1))/ (ω^2*L1^2+4*R1^2)
=(2*R1^2*(R1+2*R3)+ω^2*L1^2*R3-j*(ω*L1*R1^2+(ω^2*L1^2+4*R1^2)/(ω*C1)))/(ω^2*L1^2+4*R1^2) 式 (2.10)
Ro^2=Z1*(Z1+2*Zm)より (2.6導出済み)
Z1+2*Zm=(ω*L1*R1*(ωL1+2jR1)+2*(2*R1^2*(R1+2*R3)+ω^2*L1^2*R3-j*(ω*L1*R1^2+(ω^2*L1^2+4*R1^2)/(ω*C1))))/(ω^2*L1^2+4*R1^2)
=(ω^2*L1^2*R1+2*j*ω*L1*R1^2+4*R1^2*(R1+2*R3)+2*ω^2*L1^2*R3-2*j*(ω*L1*R1^2+(ω^2*L1^2+4*R1^2)/(ω*C1))))/(ω^2*L1^2+4*R1^2)
=(ω^2L1^2*R1+2ω^2*L1^2*R3+4R1^2(R1+2*R3)-2j(ω*L1*R1^2+(ω^2*L1^2+4*R1^2)/(ω*C1)))+2*j*ω*L1*R1^2)/(ω^2*L1^2+4*R1^2)
=( ω^2*L1^2(R1+2*R3)+4*R1^2(R1+2*R3)-2*j*(ω*L1*R1^2-ω*L1*R1^2+(ω^2*L1^2+4*R1^2)/(ω*C1)) ) /(ω^2*L1^2+4*R1^2)
=( (R1+2*R3)*(ω^2*L1^2+4*R1^2)-2*j*(ω^2*L1^2+4*R1^2)/(ω*C1) ) /(ω^2*L1^2+4*R1^2)
=(R1+2*R3)-2*j/(ω*C1)
Ro^2=Z1*(Z1+2*Zm)=R1*ω*L1*(ω*L1+2*j*R1)/(ω^2*L1^2+4*R1^2) * ( (R1+2*R3)-2j/(ω*C1) )
=((ω^2*L1^2*R1+j*2*ω*L1*R1^2)*(R1+2*R3)-2*j*(ω^2*L1^2*R1+j*2*ω*L1*R1^2)/(ω*C1)) / (ω^2*L1^2+4*R1^2)
=((ω^2*L1^2*R1)*(R1+2*R3)+(4*ω*L1*R1^2)/(ω*C1)+j*(2*ω*L1*R1^2*(R1+2*R3)-2*(ω^2*L1^2*R1)/(ω*C1))) / (ω^2*L1^2+4*R1^2)
=((ω^2*L1^2*R1)*(R1+2*R3)+(4*L1*R1^2)/C1+j*(2*ω*L1*R1*R1*(R1+2*R3)-(2*ω*L1*R1*L1/C1))) / (ω^2*L1^2+4*R1^2)
=(((ω^2*L1^2*R1)*(R1+2*R3)+(4*L1*R1^2)/C1+j*(2*ω*L1*R1*R1*(R1+2*R3)-L1/C1))) / (ω^2*L1^2+4*R1^2) 式 (2.11)
Ro=Z1(Z1+2Zm)周波数にかかわらず常に成り立つためには上記の虚数項である
(R1*(R1+2*R3)-L1/C1が0となる必要があります。
従って
L1/C1=R1*(R1+2*R3) 式 (2.12)
となります。
また実数項がRo^2になる必要があるので
((ω^2*L1^2*R1)*(R1+2*R3)+(4*L1*R1^2/C1)) / (ω^2*L1^2+4*R1^2)=Ro^2
(ω^2*L1^2*L1/C1+4*R1^2*L1/C1) / (ω^2*L1^2+4*R1^2)=Ro^2
ω^2*L1^2*L1/C1+4*R1^2*L1/C1=Ro^2*(ω^2*L1^2+4*R1^2)
ω^2*L1^3/C1+4*R1^2*L1/C1=ω^2*L1^2*Ro^2+4*R1^2*Ro^2
ω^2*L1^2(L1/C1-Ro^2)+4*R1^2(L1/C1-Ro^2)=0
(ω^2*L1^2+4*R1^2)*(L1/C1-Ro^2)=0 式 (2.13)
これを満たすためには右項である
L1/C1-Ro^2=0
を常に満たす必要があるので
L1/C1=Ro^2 式 (2.14)
L1=C1*Ro^2
C1=L1/Ro^2
R1(R1+2*R3)=Ro^2 式 (2.15)
ここまで導き出した条件はインピーダンス整合条件を満たすためのものです。
次にこのBridge-T1回路の減衰率Kについて考えてみます。
INのポイントに信号Eiを入力しBridge-T1を変換したY回路の出口の電圧をEaとします。
Kを減衰率(K>=1)とおけば
Ei=K*Ea 式 (2.16)
となります。
前項ではBridge-T1のΔ部分をY回路に変換して考えましたが、ここでは一度元のBridge-Tで考えます。
このBridge-T1回路においては周波数無限大域についてL項は無限大、C項はゼロに近づくため、この領域においては単なるR1とR3のT回路とみなすことができます。
Ztotal=R1+R3//(R1+Ro) 式 (2.17)
Ztotal=R1+R3*(R1+Ro)/(R1+R3+Ro)
Ea=Ei*R3*(R1+Ro)/(R1+R3+Ro) / (R1+R3*(R1+Ro)/(R1+R3+Ro)) * Ro/(Ro+R1)
Ea=Ei*R3*(R1+Ro) / (R1*(R1+R3+Ro)+R3*(R1+Ro)) * Ro/(Ro+R1)
Ea=Ei*R3*Ro / (R1*(R1+2*R3)+Ro*(R1+R3))
R1(R1+2*R3)=Ro^2を使って
Ea=Ei*R3*Ro / (Ro^2+Ro*(R1+R3))
Ea=Ei*R3 / (Ro+R1+R3) 式 (2.18)
EaとEiの関係が分かったのでKを求めると
K=(Ro+R1+R3)/R3 式 (2.19)
となります。ここに
R3=(Ro^2-R1^2)/(2*R1)
を代入すると
K=(Ro+R1+(Ro^2-R1^2)/(2*R1) / ((Ro^2-R1^2)/(2*R1)) 式 (2.20)
K=(2*R1*(Ro+R1)+(Ro+R1)*(Ro-R1)) / ((Ro+R1)*(Ro-R1))
K=(2*R1+(Ro-R1)) / (Ro-R1)
K=(Ro+R1)/(Ro-R1)
K*(Ro-R1)=Ro+R1
R1(K+1)=Ro(K-1)
R1=Ro*(K-1)/(K+1) 式 (2.21)
R3=(Ro^2-Ro^2(K-1)^2/(K+1)^2) / (2*Ro*(K-1)/(K+1)) = Ro*(1-(K-1)^2/(K+1)^2) / (2*(K-1)/(K+1))
=Ro*((K+1)^2-(K-1)^2)/(K+1)^2 / (2*(K-1)/(K+1)) = (Ro*4*K/(K+1)^2) / (2*(K-1)/(K+1))
=Ro*2*K/((K-1)/(K+1)*(K+1)^2) = Ro*2*K/((K+1)*(K-1)) = Ro*2*K/(K^2-1)
R3=Ro*2*K/(K^2-1) 式 (2.22)
あらためて変換後のY回路にてBridge-T1回路の伝達関数について考えます。
Bridge-T1の伝達関数Aは
A=Zm//(Z1+Ro) / (Z1+Zm//(Z1+Ro)) * (Ro/(Ro+Z1))
=(Zm*(Z1+Ro)/(Z1+Ro+Zm)) / (Z1+Zm*(Z1+Ro)/(Z1+Ro+Zm)) * (Ro/(Ro+Z1))
=Ro*Zm*(Z1+Ro) / ((Z1*(Z1+Ro+Zm)+Zm*(Z1+Ro)) / (Ro+Z1)
=Ro*Zm* / ((Z1*(Z1+Ro+Zm)+Zm*(Z1+Ro))
=Ro*Zm* / ((Z1*(Z1+Ro+2Zm)+Ro*(Z1+Zm))
=Ro*Zm / (Ro^2+Ro*(Z1+Zm))
A=Zm / (Ro+Z1+Zm) 式(2.23)
Z1=(j*ω*L1*R1)/(2*R1+j*ω*L1)
Zm= Z2+R3+1/(j*ω*C1)
= R1^2/(2*R1+j*ω*L1)+R3+1/(j*ω*C1)
=(R1^2+R3*(2*R1+j*ω*L1)+(2*R1+j*ω*L1)/(j*ω*C1))/(2*R1+j*ω*L1)
Ro+Z1+Zm=(Ro*(2*R1+j*ω*L1)+j*ω*L1*R1+(R1^2+R3*(2*R1+j*ω*L1)+(2*R1+j*ω*L1)/(j*ω*C1)))/(2*R1+j*ω*L1)
R1(R1+2*R3)=Ro^2 より
A=Zm/(Ro+Z1+Zm)
=(R1^2+R3*(2*R1+j*ω*L1)+(2*R1+j*ω*L1)/(j*ω*C1)) / (Ro*(2*R1+j*ω*L1)+j*ω*L1*R1+(R1^2+R3*(2*R1+j*ω*L1)+(2*R1+j*ω*L1)/(j*ω*C1)))
=(R1*(R1+2*R3)+R3*j*ω*L1+L1/C1+2*R1/(j*ω*C1)) / (2*Ro*R1+j*ω*L1*Ro+j*ω*L1*R1+R1*(R1+2*R3)+j*ω*L1*R3+L1/C1+2*R1/(j*ω*C1))
=(Ro^2+R3*j*ω*L1+Ro^2+2*R1/(j*ω*C1)) / (2*Ro*R1+j*ω*L1*Ro+j*ω*L1*R1+Ro^2+j*ω*L1*R3+Ro^2+2*R1/(j*ω*C1))
=(2*Ro^2+R3*j*ω*L1+2*R1/(j*ω*C1)) / (2*Ro^2+2*Ro*R1+j*ω*L1*(Ro+R1+R3)+2*R1/(j*ω*C1))
=(2*Ro^2+R3*j*ω*L1+2*R1/(j*ω*C1)) / (2*Ro*(Ro+R1)+j*ω*L1*(Ro+R1+R3)+2*R1/(j*ω*C1))
=(2*j*ω*C1*Ro^2+(jω)^2*L1*C1*R3+2*R1) / (2*j*ω*C1*Ro*(Ro+R1)+(jω)^2*L1*C1*(Ro+R1+R3)+2*R1)
=((j*ω)^2*L1*C1*R3/(2*R1)+j*ω*C1*Ro^2/R1 +1) / ((j*ω)^2*L1*C1*(Ro+R1+R3)/(2*R1)+j*ω*C1*Ro*(Ro+R1)/R1 +1) 式(2.24)
L1=C1*Ro^2を上式に代入
A=(1/2*(j*ω)^2*C1^2*Ro^2*R3/R1+j*ω*C1*Ro^2/R1 +1) / (1/2*(j*ω)^2* C1^2*Ro^2*(Ro+R1+R3)/R1+j*ω*C1*Ro*(Ro+R1)/R1 +1)
式(2.25)
式(2.21)より R1=Ro*(K-1)/(K+1)
式(2.22) より R3=Ro*2K/(K^2-1)
の二式を代入
Ro/R1=(K+1)/(K-1)
R3/R1=2*K/(K^2-1)*(K+1)/(K-1)
=2*K*(K+1)/((K^2-1)*(K-1))
=2*K/(K-1)^2
A=(1/2*(jω*)^2*C1^2*Ro^2*2*K/(K-1)^2 +j*ω*C1*Ro*(K+1)/(K-1) +1)
/ (1/2*(j*ω)^2* C1^2*Ro^2*((K+1)/(K-1) +1+2*K/(K-1)^2)+j*ω*C1*Ro*((K+1)/(K-1)+1) +1)
=((j*ω)^2*C1^2*Ro^2*K/(K-1)^2 +j*ω*C1*Ro*(K+1)/(K-1) +1)
/ (1/2*(j*ω)^2* C1^2*Ro^2*((K+1)/(K-1) +1+2*K/(K-1)^2)+j*ω*C1*Ro*((K+1)/(K-1)+1)+1)
=((j*ω)^2*C1^2*Ro^2*K/(K-1)^2+j*ω*C1*Ro*(K+1)/(K-1)+1)
/ (1/2*(j*ω)^2*C1^2*Ro^2*(((K+1)*(K-1)+(K-1)^2+2*K)/(K-1)^2)+j*ω*C1*Ro*((K+1)/(K-1)+1)+1)
=((j*ω)^2*C1^2*Ro^2*K/(K-1)^2 +j*ω*C1*Ro*(K+1)/(K-1) +1)
/ ((j*ω)^2* C1^2*Ro^2*(K^2/(K-1)^2) +j*ω*C1*Ro*((K+1)/(K-1)+(K-1)/(K-1)) +1)
=((j*ω)^2*C1^2*Ro^2*K/(K-1)^2 +j*ω*C1*Ro*(K+1)/(K-1) +1)
/ ((j*ω)^2* C1^2*Ro^2*(K^2/(K-1)^2) +j*ω*C1*Ro*(2*K/(K-1) +1)
=(j*ω*C1*Ro*K/(K-1)+1)*(j*ω*C1*Ro*1/(K-1)+1) / (*j*ω*C1*Ro*K/(K-1)+1)^2
A=(j*ω*C1*Ro*1/(K-1)+1) / (j*ω*C1*Ro*K/(K-1)+1) 式(2.26)
を導き出すことができました。
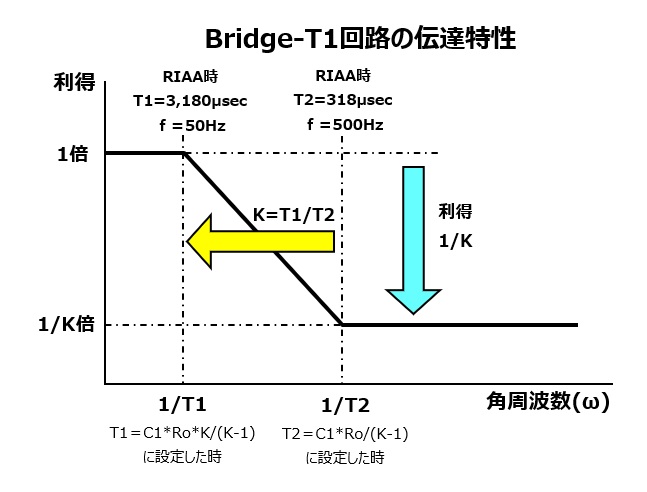
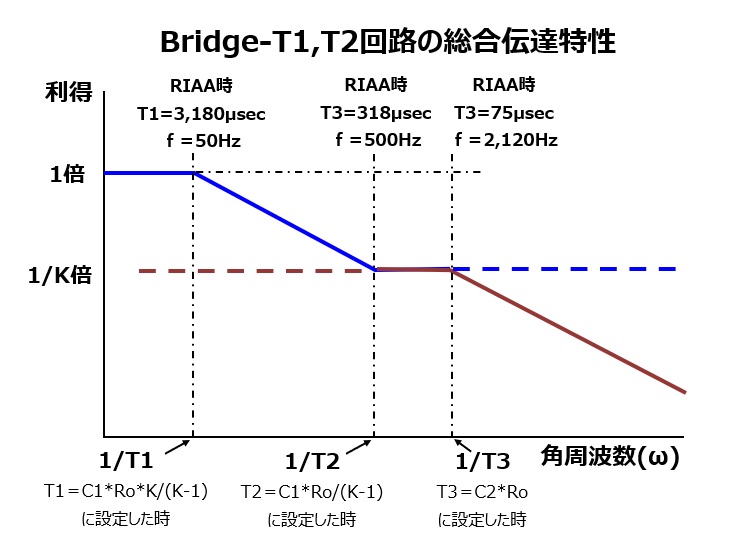
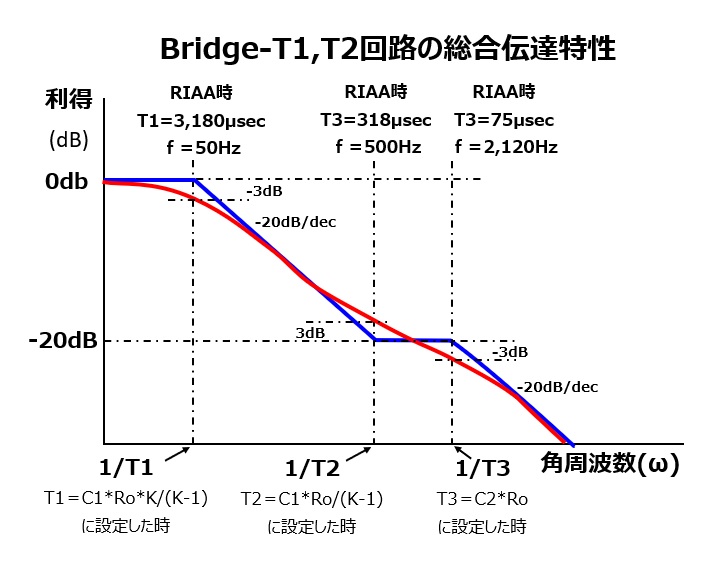
このBridge-T1回路の伝達関数Aは 1ポール(分母)、1ゼロ(分子)の特性を持ちます。この伝達関数でイコライザーの低域限界とターンオーバーを
再現しています。ロール・オフについてはBridge-T2回路にて改めて考察します。
A=(1+j*ω*C1*Ro/(K-1)) / (1+j*ω*(C1*Ro*K/(K-1))
伝達関数の分母は50Hzの低域限界を導き出すもので、分子で500Hzのターンオーバーを導き出します。
すなわち分母のωにT1、分子のωにT2との関連性をもたせて伝達関数をイコライザー特性に一致させます。
上式の伝達関数Aで
T1=K*C1*Ro/(K-1) 式(2.27)
T2=C1*Ro/(K-1) 式(2.28)
T1/T2=K*C1*Ro/(K-1) / C1*Ro/(K-1)=K 式(2.29)
となるように設定した場合伝達関数Aはどのようになるでしょうか
ωが1/T1の時
A=(j*ω*C1*Ro*1/(K-1)+1) / (j*ω*C1*Ro*K/(K-1)+1)
A(@T1)=(j*(1/T1)* C1*Ro*1/(K-1)+1) / (j*(1/T1)*C1*Ro*K/(K-1)+1)
A(@T1)=(j*(1/(K*C1*Ro/(K-1)))* C1*Ro*(1/(K-1)+1) / (j*(1/(K*C1*Ro/(K-1)))*C1*Ro*K/(K-1)+1)
A(@T1)=(j/K+1) / (j+1) 式(2.30)
|A(@T1)|=SQRT((1/K^2+1^2)/(1^2+1^2)) 式(2.31)
ωがT2の時
A(@T2)=(j*(1/T2)* C1*Ro*1/(K-1)+1) / (j*(1/T2)*C1*Ro*K/(K-1)+1)
A(@T2)=(j*(1/(C1*Ro/(K-1)))* C1*Ro*1/(K-1)+1) / (j*(1/( C1*Ro/(K-1)))*C1*Ro*K/(K-1)+1)
A(@T1)=(j+1) / (jK+1) 式(2.32)
|A(@T2)|=SQRT((1^2+1^2)/(K^2+1^2)) 式(2.33)
伝達関数Aの利得は T1 = K*C1*Ro/(K-1) より下がり始め, T2 = C1*Ro/(K-1) で 1/K になり,それ以降は平坦になります.
(即ち、周波数がK倍になると利得が1/Kになることを意味しています。)
※RIAAの場合T1/T2=3180μsec/318μsec=10であるのでK=10
|A(@T1)|=SQRT((1/100+1)/2)≒1/SQRT(2) 下降開始点(3dB落ち)
|A(@T2)|=SQRT(2/100+1) ≒ SQRT(2)/10 =SQRT(2)/K 下降終了点(1/Kまで下がりきる手前3dB高い点)
ここまでで導き出した条件からRIAA用イコライザーのBridge-T1回路を構成するLCR値を導き出します。
与件
Ro=600Ω
RIAA LCRイコライザーの場合
Low LIMIT 3180μsec T1
Turn Over 318μsec T2
Roll Off 75μsec T3 (ここでは使わない)
与件より
K= T1/T2 =10
条件より
L1/C1=Ro^2
L1=C1*Ro^2
C1=L1/Ro^2
R1*(R1+2R3)=Ro^2
R1=Ro*(K-1)/(K+1)
R3=Ro*2K/(K^2-1)
T1=K*C1*R1/(K-1)
R1=600*(10-1)/(10+1)=490.91 (Ω)
R3=600*2*10/(10^2-1)=121.21 (Ω)
C1=T1*(K-1)/(K*Ro)=3180/10000*0.9/600=0.0000477 (F)
L1=R0^2*C1=1.72 (H)
これでBridge-T1を構成するLCRの各定数が計算できました。
3. Bridge-T2回路の解析
次にBridge-T2回路について考察します。
Bridge-T2回路はBridge-T1と同じく定インピーダンスのローパスフィルタですが、この回路では高域のロールオフを実現すればよいだけ、即ち1ポール(極)のみの構成でゼロは不要となります。その結果Bridge-T1回路との相違点はR3に相当する抵抗が入っていないことです。解析を簡単に行う都合上、Bridge-T1回路のR3に相当する抵抗Rxを仮設定したうえで、最終的にRxを0にすることによりLCRの各定数を求めていきます。
まずはBridge-T1の結果の置き換えを行うと
L2/C2=Ro^2 式 (3.1)
L2=C2*Ro^2 式 (3.2)
C2=L2/Ro^2 式 (3.3)
R2*(Rx+2*Rx)=Ro^2=Z1*(Z1+2*Zm) 式 (3.4)
R2=Ro*(K-1)/(K+1) 式 (3.5)
Rx=Ro*2*K/(K^2-1) 式 (3.6)
伝達関数Aについても
A=(1+j*ω*C2*Ro/(K-1)) / (1+j*ω*(C2*Ro*K/(K-1)) 式 (3.7)
Bridge-T2の減衰率Kについてロールオフでは必要のない架空のT4をT3=75μsec(2120Hz)の1/100と設定するとKは100となります。K=100でも1/K≒0,K/(K-1)≒1といえるレベルであること、またT4をもっと小さく0に近づけていくことはいくらでも可能であるため、K=∞と設定することと同義と考えます。
ここで減衰率K=∞と設定すると
式 (3.5)より R2=Ro*(K-1)/(K+1) K⇒∞で (K-1)/(K+1)=1
従って
R2=Ro 式 (3.8)
式 (3.6)より R4=Ro*2K/(K^2-1) K⇒∞で 2K/(K^2-1)=0
従って
Rx=0 式 (3.9)
また
1/(K-1)=0, K/(K-1)=1と近似できるため。
A=(1+j*0) / (1+j*ω*(C2*Ro))
A-1 / (1+j*ω*c2*Ro) 式 (3.10)
を導き出すことができます。この伝達関数は1ポールのみ、ゼロ点なしになります。
即ちこの伝達関数はT3で規定される遮断周波数より上の帯域で、20dB/decの割合で減衰が発生します。
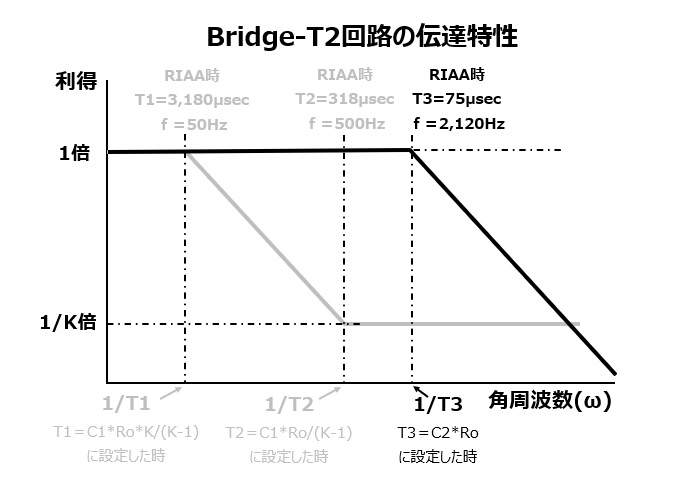
※上のグラフY軸上の1/K倍の表記はBridge-T1のものでBridge-T2とは無関係です。
Bridge-T2回路についてもRIAAイコライザ―の各種LCR設定値を計算します。
T3=C2*Ro
75(μsec)=C2*600
C2=75/600 (μF)=0.125 (μF)
L2=Ro^2*C2
より
L2=360,000*0.125*10^(-6)
=0.045 (H)
4. 全体回路の解析
Bridge-T1,T2回路を全体で見た場合、総合的な伝達関数A(total)は
A(total)=A(Bridge-T1)*A(Bridge-T2)
となりますので 式(2.26)および 式 (3.10)から
A(total)= A=(j*ω*C1*Ro*1/(K-1)+1) / ( (j*ω*C1*Ro*K/(K-1)+1) * (1+j*0) / (1+j*ω*(C2*Ro))
A(total)= A=(j*ω*C1*Ro*1/(K-1)+1) / ( (j*ω*C1*Ro*K/(K-1)+1) * (1+j*ω*C2*Ro) ) 式(4.1)
となり、伝達関数は2ポール、1ゼロを持つ形式となりました。


コメント