1. はじめに
LCR型のトーン・コントロール回路を実現するハイブースト部のLCR値を決定する方法について、やっと理論的に説明をつけることができました。LCR型トーン・コントロールの低域上昇と高域低下回路はLCRイコライザー回路でのターンオーバー部の計算方法を用いて、効き始めの周波数と上昇(下降)量を調整すればよいのですが 低域下降と高域上昇についてはLCRイコライザのターンオーバー用ブリッジT回路のLとCの挿入個所を入れ替えればよいことは、わかっているもののLCおよびRの数値の導出方法の説明ができていませんでした。今回できるだけ前回のLCRイコライザと同じ方法で証明したいと思います。
2.計算方法の導出
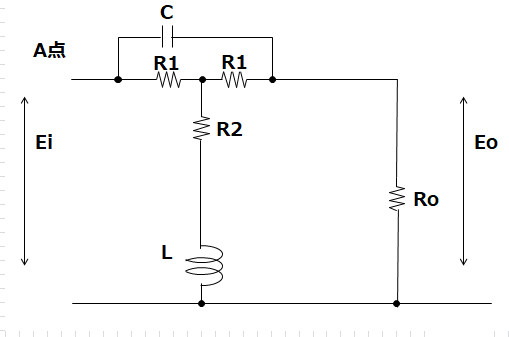
Z1=R1/(sC) / (1/(sC)+2R1)=R1 / (1+2sC*R1)
Z1=R1 / (1+2sC*R1) 式(2.1)
Z2=R1^2 /(1/(sC)+2R1)=sC*R1^2 / (1+2sC*R1)
Z2=sC*R1^2 / (1+2sC*R1) 式(2.2)
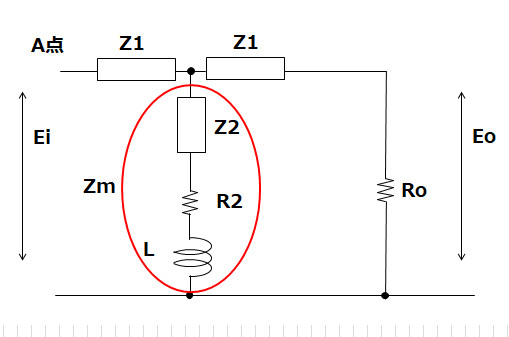
Zm=Z2+R2+sL=sC*R1^2 / (1+2sC*R1) +R2+sL
Zm=sC*R1^2 / (1+2sC*R1) +R2+sL 式(2.3)
A点から右のインピーダンス=Roとすると
Ro=Z1+Zm // (Z1+Ro)
=Z1+Zm*(Z1+Ro) /(Zm+Z1+Ro)
=[Z1*(Zm+Z1+Ro)+Zm*(Z1+Ro)] /(Zm+Z1+Ro)
=[Z1*(Zm+Z1+Ro)+Zm*(Z1+Ro)] /(Zm+Z1+Ro)
Ro=[Z1*(Zm+Z1+Ro)+Zm*(Z1+Ro)] /(Zm+Z1+Ro) 式(2.4)
Ro*( Zm+Z1+Ro)=Z1*(Zm+Z1+Ro)+Zm*(Z1+Ro)
Ro*Zm+Ro*Z1+Ro^2=2*Z1*Zm+Z1^2+Z1*Ro+Zm*Ro
Ro^2=Z1*(Z1+2*Zm) 式(2.5)
Ro^2=R1/(1+2sC*R1)*{R1/(1+2sC*R1)+2*[sC*R1^2/(1+2sC*R1) +R2+sL] }
Ro^2*(1+2sC*R1)=R1*{R1/(1+2sC*R1)+2*[sC*R1^2/(1+2sC*R1) +R2+sL] }
Ro^2*(1+2sC*R1)=R1*{R1/(1+2sC*R1) +2*[sC*R1^2/(1+2sC*R1) +(R2+sL)*(1+2sC*R1)/(1+2sC*R1)]}
Ro^2*(1+2sC*R1)^2=R1*{R1+2*[sC*R1^2+(R2+sL)*(1+2sC*R1)] }
Ro^2*(1+2sC*R1)^2=R1*{R1+2sC*R1^2+2*(R2+sL)*(1+2sC*R1) }
Ro^2*(1+(2sC*R1)^2+4sC*R1)=
R1^2+2sC*R1^3+2R1*R2+4sC*R1^2*R2+2sL*R1+4s^2*C*R1^2*L
Ro^2+Ro^2*(2sC*R1)^2+Ro^2*4sC*R1=
R1^2+2sC*R1^3+2R1*R2+4sC*R1^2*R2+2sL*R1+4s^2*C*R1^2*L
Ro^2+(2sC*R1*Ro)^2+4sC*R1* Ro^2=
R1^2+2R1*R2+2sR1*(C*R1^2+2C*R1*R2+sL)+4s^2C*R1^2*L
式(2.6)
s (=jω) 一次項の比較 虚数軸の比較
s*4C*R1*Ro^2=s*2*R1*(C*R1^2+2C*R1*R2+L)
が抜き出せます。
2Ro^2=R1^2+2R1*R2+L/C=R1*(R1+2R2)+L/C
2Ro^2=R1*(R1+2R2)+L/C 式(2.7)
次にsなし項の比較します。 実数軸の比較
ここで S^2=(jω)^2=-ω^2
Ro^2-4ω^2*C^2*R1^2*Ro^2=R1^2+2R1*R2-4ω^2*C*R1^2*L
上式からωに依存しない項を抽出すると
Ro^2=R1^2+2R1*R2=R1*(R1+2R2)
Ro^2=R1*(R1+2R2) 式(2.8)
が導き出され
ωに依存する項を抽出すると
4ω^2*C^2*R1^2*Ro^2=4ω^2*C*R1^2*L
Ro^2=LC/C^2=L/C
Ro^2=L/C 式(2.9)
が導き出されます
式(2.8)を変形すると
R2=(Ro^2-R1^2)/(2R1) 式(2.10)
となります。
次にこの回路の減衰率K(>=1)について考察します。
Eo=Ro/(Z1+Ro) * Zm//(Z1+Ro) / [Z1+Zm//(Z1+Ro)] *Ei
Eo/Ei=K (K>=1 :減衰率)
Eo=Ro/(Z1+Ro) * Zm//(Z1+Ro) / Ro *Ei
Eo=Zm//(Z1+Ro) / (Z1+Ro) *Ei
Eo=Zm*(Z1+Ro)/(Zm+Z1+Ro) / (Z1+Ro) *Ei
Eo=Zm/(Zm+Z1+Ro) *Ei 式(2.11)
Ei/Eo=K= (Zm+Z1+Ro) / Zm 式(2.12)
周波数0の時の減衰率 Kを考えます。
Ei/Eo=K= (Zm+Z1+Ro) / Zm
ω=0時には
Zm=R2, Z1=R1
となるので
Ei/Eo=K= (Zm+Z1+Ro) / Zm は
K=(R2+R1+Ro)/R2 となります。
K=(R2+R1+Ro)/R2に
R2=(Ro^2-R1^2)/(2R1)を代入すると
K=[(Ro^2-R1^2)/(2R1)+R1+Ro]/[ (Ro^2-R1^2)/(2R1)]
=[2R1*( R1+Ro)+(Ro^2-R1^2)] /(Ro^2-R1^2)
=[2R1*Ro+(Ro^2+R1^2)] /[(Ro+R1)*(Ro-R1)]
=[(Ro+R1)^2] /[(Ro+R1)*(Ro-R1)]
=(Ro+R1)/(Ro-R1)
K*(Ro-R1)=Ro+R1
Ro*(K-1)=R1*(K+1)
R1=(K-1)/(K+1) *Ro 式(2.13)
式(2.10)のR2=(Ro^2-R1^2)/(2R1)に
式(2.13)で導きだしたR1を代入すると
R2=(Ro- ( (K-1)^2/(K+1)^2*Ro) / (2(K-1)/(K+1))
R2=(Ro*(K+1)- ( (K-1)^2/(K+1)*Ro) / (2(K-1))
R2=(Ro*(K+1)/(K-1)- ( (K-1)/(K+1)*Ro) /2
R2=1/2* ( Ro*(K+1)/(K-1)- (K-1)/(K+1)*Ro )
R2=1/2*Ro*[ (K+1)/(K-1)-(K-1)/(K+1) ]
R2=1/2*Ro*[ ((K+1)*(K+1)/(K+1)*(K-1)) – (K-1)*(K-1)/( (K+1)*(K-1) ) ]
R2=1/2*Ro*[ (4K/(K^2-1) ]
R2=2*Ro*K/(K^2-1) 式(2.14)
次に回路の伝達関数Aについて考えます。
式(2.11)より
Eo=Zm / (Zm+Z1+Ro) *Ei
Aの定義は Eo=A*Eiであるので
A=Zm / (Ro+Z1+Zm)
となります。そこにこれまで導出した以下の3式
Ro^2=R1(R1+2R2)=L/C
R1=Ro*(K-1)/(K+1)
R2=2Ro*K/(K^2-1)
を代入すると
A=Zm/(Ro+Z1+Zm)
={sC*R1^2 / (1+2sC*R1) +R2+sL} / {Ro+ R1/(1+2sC*R1) + sC*R1^2 / (1+2sC*R1) +R2+sL}
={sC*R1^2+(1+2sC*R1)*(R2+sL)} / {R1+sC*R1^2+(1+2sC*R1)*( Ro+R2+sL)}
={sC*R1^2+(1+2sC*R1)*(R2+sC*Ro^2) } / {R1+sC*R1^2+(1+2sC*R1)*( Ro+R2+sC*Ro^2)}
={sC*R1^2+2sC*R1*(R2+sC*Ro^2)+(R2+sC*Ro^2)} /
{R1+sC*R1^2+2sC*R1*(Ro+R2+sC*Ro^2)+ (Ro+R2+sC*Ro^2)}
={sC*R1*(R1+2*(R2+sC*Ro^2)+(R2+sC*Ro^2)} /
{sC*R1*(R1+2*(Ro+R2+sC*Ro^2)+ (Ro+R1+R2+sC*Ro^2)}
={sC*R1*(R1+2*R2)+2sC*R1*sC*Ro^2)+(R2+sC*Ro^2)} /
{sC*R1*(R1+2R2)+2sC*R1*(Ro+sC*Ro^2)+ (Ro+R1+R2+sC*Ro^2)}
={sC*Ro^2+2sC*R1*sC*Ro^2)+(R2+sC*Ro^2)} /
{sC*Ro^2+2sC*R1*(Ro+sC*Ro^2)+ (Ro+R1+R2+sC*Ro^2)}
={sC*Ro^2*(2+2sC*R1)+R2} / {sC*Ro^2*(2+2sC*R1)+2sC*Ro*R1+ (Ro+R1+R2)}
={sC*Ro^2*(2+2sC* Ro*(K-1)/(K+1))+R2} /
{sC*Ro^2*(2+2sC* Ro*(K-1)/(K+1))+2sC*Ro* Ro*(K-1)/(K+1)+ (Ro+Ro*(K-1)/(K+1)+R2)}
={sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+R2*(K+1)} /
{sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+2sC*Ro* Ro*(K-1)+ (Ro+R2) *(K+1)+Ro*(K-1)}
={sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+ 2*(K+1)*Ro*K/(K^2-1)} /
{sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+2sC*Ro* Ro*(K-1)+ (Ro+2Ro*K/(K^2-1)) *(K+1)+Ro*(K-1)}
={sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+ 2*(K+1)*Ro*K/[(K+1)*(K-1)]} /
{sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+2sC*Ro^2*(K-1)+ (Ro+2Ro*K/[(K+1)*(K-1)]) *(K+1)+Ro*(K-1)}
={sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+ 2*(K+1)*Ro*K/[(K+1)*(K-1)]} /
{sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+2sC*Ro^2*(K-1)+ (Ro+2Ro*K/[(K+1)*(K-1)]) *(K+1)+Ro*(K-1)}
={sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+ 2*(K+1)*Ro*K/[(K+1)*(K-1)]} /
{sC*Ro^2*(2*(K+1)+2*(K-1)+2sC*Ro*(K-1))+ (2Ro*K/[(K+1)*(K-1)]) *(K+1)+Ro*(K-1)+Ro*(K+1)}
={sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+ 2*(K+1)*Ro*K/[(K+1)*(K-1)]} /
{sC*Ro^2*(4K+2sC* Ro*(K-1))+ (2Ro*K/[(K+1)*(K-1)]) *(K+1)+2K*Ro}
={sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+ 2*Ro*K/(K-1)} /
{sC*Ro^2*(4K+2sC* Ro*(K-1))+ (2Ro*K/[(K+1)*(K-1)]) *(K+1)+2K*Ro}
={sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+ 2*Ro*K/(K-1)} /
{sC*Ro^2*(4K+2sC* Ro*(K-1))+ 2Ro*K/(K-1) +2K*Ro}
={sC*Ro^2*(2*(K+1)+2sC* Ro*(K-1))+ 2*Ro*K/(K-1)} /
{sC*Ro^2*(4K+2sC* Ro*(K-1))+ 2Ro*K/(K-1) +2K*Ro}
分母と分子をRoで割ると
={sC*Ro*(2*(K+1)+2sC* Ro*(K-1))+ 2*K/(K-1)} / {sC*Ro*(4K+2sC* Ro*(K-1))+ 2*K/(K-1)+2K}
その上に分母分子を2で割ると
={sC*Ro*((K+1)+sC* Ro*(K-1))+ K/(K-1)} / {sC*Ro*(2K+sC* Ro*(K-1))+ K/(K-1) +K}
={sC*Ro*((K+1)+sC* Ro*(K-1))+ K/(K-1)} / {sC*Ro*(2K+sC* Ro*(K-1))+ K/(K-1) +K*(K-1)/(K-1)}
={sC*Ro*((K+1)+sC* Ro*(K-1))+ K/(K-1)} / {sC*Ro*(2K+sC* Ro*(K-1))+ (K^2-K+K)/(K-1)}
={sC*Ro*((K+1)+sC* Ro*(K-1))+ K/(K-1)} / {sC*Ro*(2K+sC* Ro*(K-1))+ K^2/(K-1)}
カッコをばらすと
={sC*Ro*(K+1)+(sC*Ro)^2*(K-1)+ K/(K-1)} / {sC*Ro*2K+(sC*Ro)^2*(K-1)+ K^2/(K-1)}
={ (sC*Ro)^2*(K-1)+ sC*Ro*(K+1)+ K/(K-1)} / { (sC*Ro)^2*(K-1)+ 2sC*Ro*K+ K^2/(K-1)}
分母分子に(K-1)/K^2を乗ずると
={ (sC*Ro)^2*(K-1)*(K-1)/K^2+ sC*Ro*(K+1)*(K-1)/K^2+ K/(K-1)*(K-1)/K^2} /
{ (sC*Ro)^2*(K-1)*(K-1)/K^2+ 2sC*Ro*K*(K-1)/K^2+ K^2/(K-1)*(K-1)/K^2}
={ (sC*Ro)^2*(K-1)^2/K^2+ sC*Ro*(K+1)*(K-1)/K^2+ 1/K} /
{ (sC*Ro)^2*(K-1)^2/K^2+ 2sC*Ro*(K-1)/K+ 1}
={ ( sC*Ro*(K-1)/K )^2+ sC*Ro*(K+1)*(K-1)/K^2+ 1/K } /
{ ( sC*Ro*(K-1)/K )^2+ 2sC*Ro*(K-1)/K+ 1 }
={ ( sC*Ro*(K-1)/K )^2+ sC*Ro*(K+1)*(K-1)/K^2+ 1/K } /
{ ( sC*Ro*(K-1)/K +1 )^2-2sC*Ro*(K-1)/K + 2sC*Ro*(K-1)/K }
={ sC*Ro*(K-1)/K*( sC*Ro*(K-1)/K + (K+1)/K ) + 1/K } /
{ ( sC*Ro*(K-1)/K +1 )^2 }
=1/K^2*{ sC*Ro*(K-1)*[sC*Ro*(K-1)+(K+1)]+K } / { ( sC*Ro*(K-1)/K +1 )^2 }
=1/K^2*{ sC*Ro*(K-1)*[K*(sC*Ro+1)–sC*Ro+1]+K } / { ( sC*Ro*(K-1)/K +1 )^2 }
=1/K^2*{ sC*Ro*(K-1)*[K*sC*Ro+K–sC*Ro+1]+K } / { ( sC*Ro*(K-1)/K +1 )^2 }
=1/K^2*{ sC*Ro*(K-1)*[K*sC*Ro–sC*Ro+K +1]+K } / { ( sC*Ro*(K-1)/K +1 )^2 }
=1/K^2*{ sC*Ro*(K-1)*[sC*Ro*(K-1)+K +1]+K } / { ( sC*Ro*(K-1)/K +1 )^2 }
={ ( sC*Ro*(K-1)/K )^2+ sC*Ro*(K+1)*(K-1)/K^2+ 1/K } / { ( sC*Ro*(K-1)/K +1 )^2 }
={ ( sC*Ro*(K-1)/K +1 )^2 -2*sC*Ro*(K-1)/K + sC*Ro*(K+1)*(K-1)/K^2+ 1/K -1 } /
{ ( sC*Ro*(K-1)/K +1 )^2 }
={ ( sC*Ro*(K-1)/K +1 )^2 + sC*Ro*(K-1)/K*(-2+(K+1)/K ) – (K-1)/K } /
{ ( sC*Ro*(K-1)/K +1 )^2 }
={ ( sC*Ro*(K-1)/K +1 )^2 – sC*Ro*(K-1)^2/K^2 – (K-1)/K } /
{ ( sC*Ro*(K-1)/K +1 )^2 }
={ ( sC*Ro*(K-1)/K +1 )^2 – (K-1)/K*(sC*Ro*(K-1)/K +1) } / { ( sC*Ro*(K-1)/K+1 )^2 }
={ sC*Ro*(K-1)/K +1-(K-1)/K }*(sC*Ro*(K-1)/K +1) / { ( sC*Ro*(K-1)/K +1 )^2 }
={ sC*Ro*(K-1)/K +1- (K-1)/K } / ( sC*Ro*(K-1)/K +1 )
={ sC*Ro*(K-1)/K +1/K } / ( sC*Ro*(K-1)/K +1 )
=1/K*( sC*Ro*(K-1) +1 ) / ( sC*Ro*(K-1)/K +1 )
=( sC*Ro*(K-1) +1 ) / { K* ( sC*Ro*(K-1)/K +1 ) }
A =( sC*Ro*(K-1) +1 ) / ( sC*Ro*(K-1) +K )
A=1/K*{ sC*Ro*(K-1) +1 } / ( sC*Ro*(K-1)/K +1 ) 式(2.15)
ついにこの回路の伝達関数Aが導き出せました。
これは通常のLCR-EQのターンオーバー部の伝達関数と似た形にまとまっています。
A=( sC1*Ro*1/(K-1)+1) / ( sC1*Ro*K/(K-1)+1) (通常のLCR-EQのターンオーバー部)
イコライザ同様の20dBの減衰は多分必要ないかとは思いますが、導き出したハイブーストの伝達関数が正解かどうかK=10で確かめてみたいと思います。
式(2.16)で導き出した伝達関数
A=1/K*{ sC*Ro*(K-1) +1 } / ( sC*Ro*(K-1)/K +1 )
に s=jωを代入します。
A =( jωC*Ro*(K-1) +1 ) / (jωC*Ro*(K-1) +K )
A =1/K*( jωC*Ro*(K-1) +1 ) / (jωC*Ro*(K-1)/K +1 )
T1=C*Ro*(K-1)
T2=C*Ro*(K-1)/K
であるため上式Aは
A=1/K*(jωT1+1)*(jωT2+1) 式(2.16)
C=T1/(Ro*(K-1) ) 式(2.17)
A=1/K*{ jωC*Ro*(K-1) +1 } / ( jωC*Ro*(K-1)/K +1 )
ω=1/T1の時
A(@T1)=1/K*{ j/( C*Ro*(K-1) )*C*Ro*(K-1) +1 } / ( j/( C*Ro*(K-1) )*C*Ro*(K-1)/K +1 )
A(@T1)=1/K*[ (j+1 / (j/K +1) ]
|A(@T1)|=1/K*SQRT((1^2+1^2)/(1/K^2+1^2))=1/K*SQRT(2/(1/K^2+1))
K=10
≒1/K*SQRT(2/(1/K^2+1)
=1/K*SQRT(2)
が導き出され ω=1/T1の時、利得は1/K(ただし√2倍は3dB上昇点)となりました。
また、
ω=1/T2の時
A(@T2)=1/K*{ j/( C*Ro*(K-1)/K )*C*Ro*(K-1) +1 } / ( j/( C*Ro*(K-1)/K )*C*Ro*(K-1)/K +1 )
A(@T2)=1/K*[ (jK+1 / (j +1) ]
|A(@T2)|=1/K*SQRT((K^2+1^2)/(1^2+1^2))=1/K*SQRT((K^2+1)/2)
K=10
≒1/K*SQRT((K^2)/2)
=1/SQRT(2)
となり、このポイントが利得1から3dB下がったポイントであることを示しています。(1/√2倍)
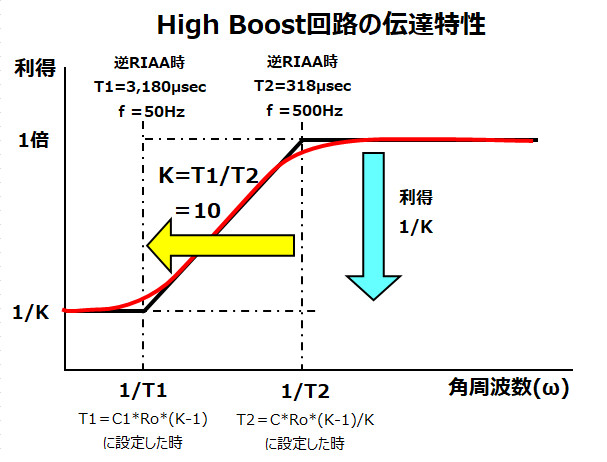
※このグラフはK=10のため、逆RIAAをイメージして作成しました。
以上、全ての計算が証明されました。
必要なLCR値を求めるのに必要な計算式は以下の通りです。
Ro^2=L/C 式(2.9)
R1=(K-1)/(K+1) *Ro 式(2.13)より
R2=2*Ro*K/(K^2-1) 式(2.14)より
C=T1/ (Ro*(K-1) ) 式(2.17)より
L=C*Ro^2
L=T1/ (Ro*(K-1))*Ro^2
L=T1*Ro/(K-1) 式(2.18)
記事の本編は以上です。
ここで導き出したC,L値は
C=T1/ (Ro*(K-1) )
L=T1*Ro/(K-1)
ですが、以前の記事との整合性が取れていません。
以前の記事ではC1,L1をT2から導き出し
K=T1/T2 (T1>T2)
C1= T2(μsec)*1.224*10^(-6)*K / ((K-1)*Ro) (F)
C1= T2(μsec)*1.224*K / ((K-1)*Ro) (μF)
L1=T2(μsec)*1.224*10^(-6)*Ro*K / (K-1) (H)
としていたため、今回の記事のL,C導出をT1からT2に変更するとT1=K*T2となるためそれを代入すると
C=T1/ (Ro*(K-1) )
C=T2*K/ (Ro*(K-1) )
L=T1*Ro/(K-1)
L=T2*K*Ro/(K-1)
となり、例の謎の定数1.224が消えていますが、それ以外は同じ結果が導き出せました。
今回導出したL,C値をシミュレーターに入れると利得特性グラフのくびれのポイントが周波数軸で高い方に若干ずれが生ずるためそれを補正するのにちょうどいい値が1.224でした。実際はそのずれによってクリティカルなほどの特性差は生じないため、以前の記事から、この1.224関連の部分は訂正線をかけ、削除することにします。
6/14 追記: ついに1.224の原因が判明しました。LRCの数値を代入して利得を計算するエクセルシミュレータの計算式が間違っていました。このシミュレータはLCRイコライザの計算のため作成して、今回ブリッジTの LとCを入れ替えたのですが、1/jωCの分母にjをかけた際に符号を反転するのを忘れたため計算が狂ってしまっていました。LCRトーンコントローラーの記事で示したグラフも間違っており、それをベースとしたLC値も正確ではないということになります。近いうちにそちらの記事も訂正します。


コメント